第 1 頁 (共 2 頁)
94年彰化第2,5,12,19,20題
發表於 : 2009年 7月 8日, 10:40
由 choice0818
麻煩以及謝謝thepiano老師了
Re: 94年彰化第2,5,12,19,20題
發表於 : 2009年 7月 8日, 15:32
由 thepiano
Re: 94年彰化第2,5,12,19,20題
發表於 : 2009年 7月 9日, 11:30
由 choice0818
請問第2題不是應該是sin嗎 為何是tan(如圖)
謝謝
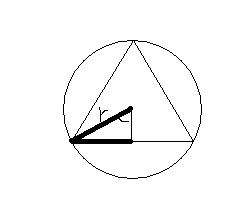
- 1.JPG (5.38 KiB) 已瀏覽 29929 次
Re: 94年彰化第2,5,12,19,20題
發表於 : 2009年 7月 9日, 11:36
由 choice0818
第五題的正確解答是1/5[2 -3]
[-1 4 ] 嗎
Re: 94年彰化第2,5,12,19,20題
發表於 : 2009年 7月 9日, 14:37
由 thepiano
choice0818 寫:第五題的正確解答是1/5[2 -3]
[-1 4 ] 嗎
對
Re: 94年彰化第2,5,12,19,20題
發表於 : 2009年 7月 9日, 14:38
由 thepiano
choice0818 寫:請問第2題不是應該是sin嗎 為何是tan
正 n 邊形在圓的外面才對
94年彰化第1、5、18、19題
發表於 : 2012年 11月 11日, 12:30
由 shih_hui3
第一題有看過駭客的解法是
令x=2+3i
所以(x-2)^2=(3i)^2 所以x^2-4x+13=0
我忘記這個步驟是什麼了>"<
第5題是我看連結失效了QQ
第18題不太懂駭客的解法>"<
第19題我算出來答案是7/5 可是選項沒有這個答案耶?
謝謝鋼琴老師:)
Re: 94年彰化第2,5,12,19,20題
發表於 : 2012年 11月 11日, 15:00
由 thepiano
第 1 題
實係數方程式,虛根必成對
有一根 2 + 3i,必有一根是 2 - 3i
剩下一個根就是實數,故 y = g(x) 之圖形與 x 軸僅有 1 交點
第 5 題
求反矩陣是基本題,可參考
http://csm01.csu.edu.tw/0166/Math3/63.htm
第 18 題
y = kx^2 + 4x + k ≧ 0 無解
表示 y = kx^2 + 4x + k < 0
整個函數圖形在 x 軸下方
k < 0
4^2 - 4 * k * k < 0
...
第 19 題
在 L_1 上找一點 A(0,5/4)
求出 A 到 L_2 之距離 = 7/5
這是基本題,留給您練習
Re: 94年彰化第2,5,12,19,20題
發表於 : 2012年 11月 11日, 17:47
由 shih_hui3
dear鋼琴老師
第19題我有算出來喔!
只是選項只有(1)2 (2)5 (3)7 (4)8
然後公佈答案是3
所以是答案錯了嗎?
Re: 94年彰化第2,5,12,19,20題
發表於 : 2012年 11月 11日, 21:03
由 thepiano
當年這份試題有 5 題送分
答案請參考附件